코랩 사용해보기

셀 경계에 마우스를 올려 코드 또는 텍스트를 추가할 수 있다.
코드를 입력하고 Ctrl+Enter를 누르면 실행되고, 그 결과는 아래에 나타난다.
cf. Shift+Enter는 셀 실행 후 다음 셀 이동
Alt+Enter는 셀 실행 후 아래 new 셀 삽입
넘파이(NumPy)
파이썬 리스트 복습

파이썬 리스트의 인덱스는 0부터 시작한다.
2번 인덱스를 출력하면 3번째 값이 출력된다.

리스트를 중첩해서 2차원 배열 만들 수 있다.
배열의 요소를 선택할 때는 2개의 []를 사용한다.
첫 번째는 행을, 두 번째는 열을 선택한다.
NumPy 준비

코랩에 넘파이가 설치되어 있어 import 해서 사용할 수 있다.
__version__으로 버전을 확인할 수 있다.
내가 사용하는 버전은 1.19.5이다.
넘파이로 배열 만들기
*넘파이는 배열에 숫자, 문자열을 함께 담을 수 없다.
1. array() 함수로 2차원 배열 생성

array() 함수로 배열을 생성할 수 있다.
2행 3열의 배열을 생성하고 출력했다. 출력하면 열과 행이 맞춰져서 출력된다.
2. type() 함수로 넘파이 배열인지 확인

type() 함수로 타입을 확인할 수 있다.
3. 넘파일 배열에서 요소 선택

파이썬 리스트와 동일하게 []에 숫자를 넣어 요소를 선택할 수 있다.
4. 넘파이 내장 함수 사용

넘파이 내장함수 sum()은 매개변수로 들어온 것의 모든 요소를 더한 값으 출력한다.
my_arr는 10, 20, 30, 40, 50, 60을 요소로 가지고 있고, sum() 함수에 넣으면 합계 210이 출력된다.
맷플롯립(Matplotlib)으로 그래프 그리기

맷플롯립도 코랩에 설치되어 있어 import 해서 사용할 수 있다.
1. 선 그래프 그리기
x축, y축 값을 plot() 함수에 전달하고, show() 함수로 그래프를 출력할 수 있다.

show() 안 했는데도 보이네?? 했는데 그 답이 다음줄에 있었네 ㅋㅋㅋ
show() 안 해도 미리보기로 보여주지만 show() 사용하면 더 깔끔하고 보기 좋은 그래프로 보여준다고 한다.
2. 산점도 그리기
산점도는 데이터의 x축, y축 값을 이용하여 점으로 그린 것이다.

3. 넘파이 배열로 산점도 그리기
넘파이의 random.randn() 함수는 표준 정규 분포를 따르는 난수를 생성하는 함수이다.
random.randn() 함수의 매개변수는 생성할 난수의 개수이다.

선형 회귀
y=ax+b,
이 1차 함수의 기울기는 a이고 절편은 b다.
선형회귀는 기울기와 절편을 찾아낸다.
x, y 값이 주어지고 해당하는 일차함수 그래프를 찾으면 그것은 '최적화 된 선형 회귀로 만든 모델'이 된다.
최적화 된 선형 회귀 모델을 찾으면 새 입력에 대한 어떤 값을 예측할 수 있다.
데이터 가져와 문제 해결하기
1. load_diabetes() 함수로 당뇨병 데이터 준비하기

사이킷런에서 당뇨병 환자 데이터 가져왔다.
load_diabetes() 함수를 임포트한 후 매개변수를 넣지 않고 호출하면 데이터가 저장된다.
데이터의 자료형은 딕셔너리와 유사한 Bunch 클래스이다.
2. 입력과 타깃 데이터의 크기 확인하기

shape 속성은 배열의 크기를 나타낸다.
data은 442*10 크기의 배열이고, target은 442개 요소를 가진 것을 확인할 수 있다.
data에서 행은 샘플이고, 열은 샘플의 특성이다.
3. 입력 데이터 자세히 보기

0번째 부터 3개의 데이터를 출력했다.
한 데이터는 10개의 특성을 가지고 있다는 것을 알 수 있다.
4. 타깃 데이터 자세히 보기

이번에도 0번째부터 3개의 값을 출력했다.
당뇨병 환자 데이터 시각화 하기
1. 맷플롯립의 scatter() 함수로 산점도 그리기
당뇨병 데이터 세트는 10개의 특성이 있고, 이 특성을 모두 그래프로 표현하려면 고차원 그래프가 필요하다.
그래서, 1개의 특성만 사용하여 그릴 것이다.

x축은 3번째 특성이고, y축은 타겟이다.
그래프를 보면 3번째 특성과 y축이 정비례 관계임을 알 수 있다.
2. 훈련 데이터 준비하기

데이터의 3번째 특성과 타겟을 따로 분리해서 변수에 저장해서 사용할 수 있다.
경사 하강법
선형회귀의 목표는 입력 데이터와 타겟 데이터를 통해 기울기와 절편을 찾는 것이다.
경사하강법은 모델이 데이터를 잘 표현할 수 있도록 기울기를 사용하여 모델을 조금씩 조정하는 최적화 알고리즘이다.
예측값과 변화율
딥러닝 분야에서 기울기 a를 가중치를 의미하는 w나 계수를 의미하는 θ로 표기한다.
y는 y^(와이 햇; 착한 사람 눈에만 ^가 y위에 있다.)으로 표기한다.
y^=wx+b에서 가중치 w와 절편 b는 알고리즘이 찾는 규칙을 의미하고, y^은 예측값이다.
* 예측값: 모델에 어떤 값을 넣었을 때 나오는 출력 값
예측값으로 올바른 모델 찾기
<훈련 데이터와 잘 맞는 가중치와 절편 찾는 방법>
① 무작위로 w, b 정한다.
② x에서 샘플 하나 선택해 y^ 계산한다.
③ y^과 선택한 샘플의 y 비교
④ y^와 y가 가까워지도록 w, b 조정
⑤ 모든 샘플을 처리할 때까지 다시 ②~④반복
1. w, b 초기화

아직 규칙을 정하지 않았으니, 일단 그냥 1.0으로 초기화
2. 훈련 데이터의 첫 번째 샘플 데이터로 y^ 얻기

첫 번째 샘플 x[0]의 y^을 얻었다.
3. 타깃과 예측 데이터 비교

y^(1.061....)과 y(151.0)가 차이가 많이 난다.
w값 조절이 필요한 것 같다.
4. w값 조절해 예측값 수정

w를 0.1를 증가하고 y^를 확인해보니 이전과 0.005정도 차이나는 거 같다.
5. w값 조정 후, 예측값 증가 정도 확인코랩 사용해보기

y^의 증가량을 w 증가량으로 나누면 얼마나 증가했는지 알 수 있다.
결과가 양수이므로 w를 증가시켜야 한다.(음수이면 w를 감소해야 한다.)
w=w+w 증가량(변화량)
변화율로 절편 업데이트

b를 0.1만큼 증가시키고 y_hat의 변화율을 계산한다.
변화율이 1이 나왔다.

절편에 변화율을 더해 b_new를 만들었다.
오차 역전파로 가중치와 절편을 적절히 업데이트
오차 역전파(오차가 연이어 전파)는 y^과 y의 차를 이용해 w, b를 업데이트 한다.
1. 오차와 변화율을 곱해 가중치 업데이트

w 변화율, b 변화율에 오차를 곱한 다음, w_new, b_new를 출력했다.
w, b 모두 크게 바뀌었다.
2. 오차를 구해 새 w, b 구하기

3. 전체 샘플 반복

앞선 과정을 반복문 안에 넣어 전체 샘플에서 하게 한다.
4. 산점도로 확인

흐음... 아직 좀 많이 부족한 거 같구만..
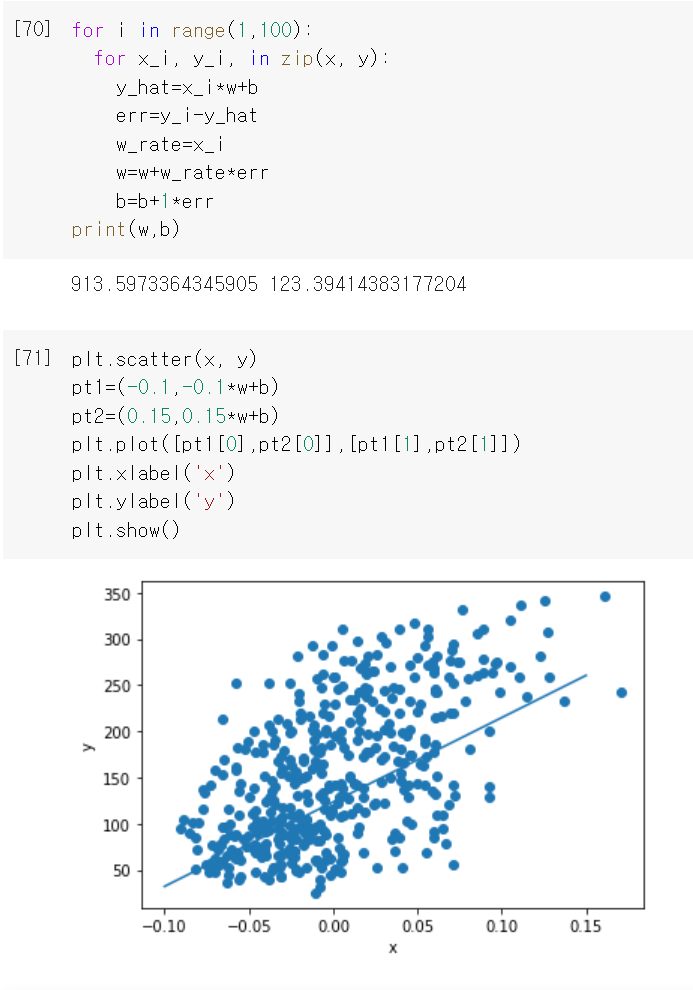
5. 여러 에포크 반복
*에포크: 전체 훈련 데이터를 모두 이용해 한 단위 작업을 진행하는 것
6. 모델로 예측랩 사용해보기

x가 0.18일 때 y^ 값을 예측했더니 287.8416....이 나왔다.

예측한 값을 산점도에 표현하면 위와 같다
'STUDY > 인공지능' 카테고리의 다른 글
| [6주차] 신경망 알고리즘 벡터화 (0) | 2021.05.25 |
|---|---|
| [5주차] 규제 방법, 교차검증 (0) | 2021.05.17 |
| [4주차] 검증세트, 전처리, 과대적합과 과소적합 (0) | 2021.05.11 |
| [3주차]데이터 세트 분류, 로지스틱 회귀과 단일층 신경망 관계 (0) | 2021.05.04 |
| [2주차] 손실함수와 경사하강법의 관계, 선형회귀를 위한 클래스 생성, 퍼셉트론, 아달린, 로지스틱 회귀, 시그모이드 함수, 로지스틱 손실 함수 (0) | 2021.04.02 |



